Technical Specifications
Delve into the intricate details and specifications that power Elusiv's groundbreaking privacy protocol and the Warden Network, enhancing blockchain transaction security and compliance.
Commitment Schemes
Homemade commitment scheme
Alice and Bob have their own Friday night tradition: they like to order pizza. They are also players, so Bob offers a deal to Alice if she can guess which pizza Bob will order she will get a slice of it, otherwise, Bob can take one slice of Alice’s pizza. Alice agrees to that deal and instantly bets that Bob is ordering a pepperoni pizza as usual. It turns out, however, that Bob wants to order a pizza Margherita. After begrudgingly handing over one of her slices, Alice suspects Bob is cheating. However, they are stuck with this game as whoever goes first reveals the pizza the other should not order to get an extra slice.
Instead, Alice proposes the following variant: Bob must first secretly write down his order, place it in a locked safe while keeping the key, and give the locked safe to Alice (Figure 3).
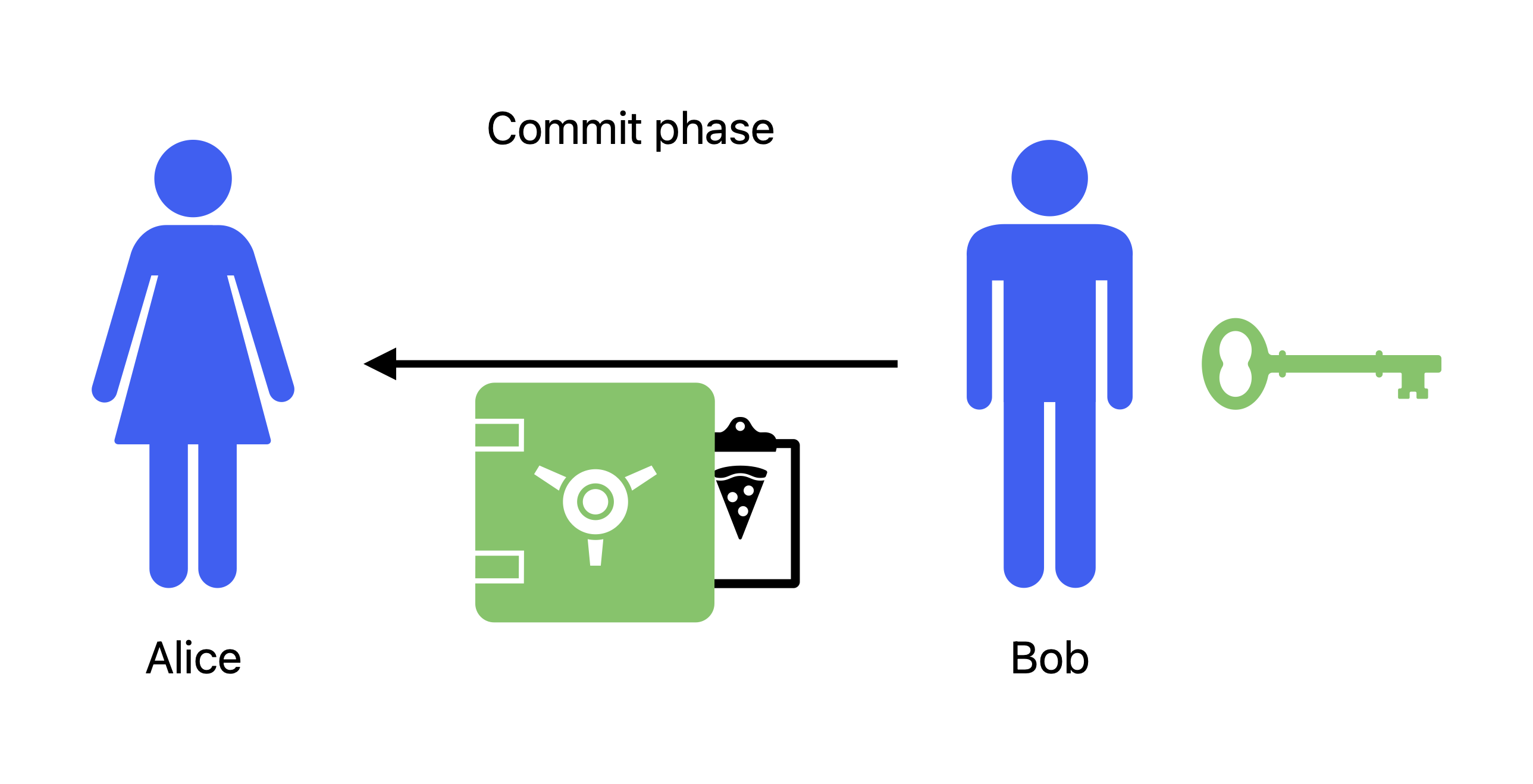
Figure 3
She can now announce her pepperoni pizza guess without fearing her friend to maliciously change his mind, as his order is securely stored in the safe. They can then open the safe together and observe that Bob was going for the pepperoni pizza (Figure 4).
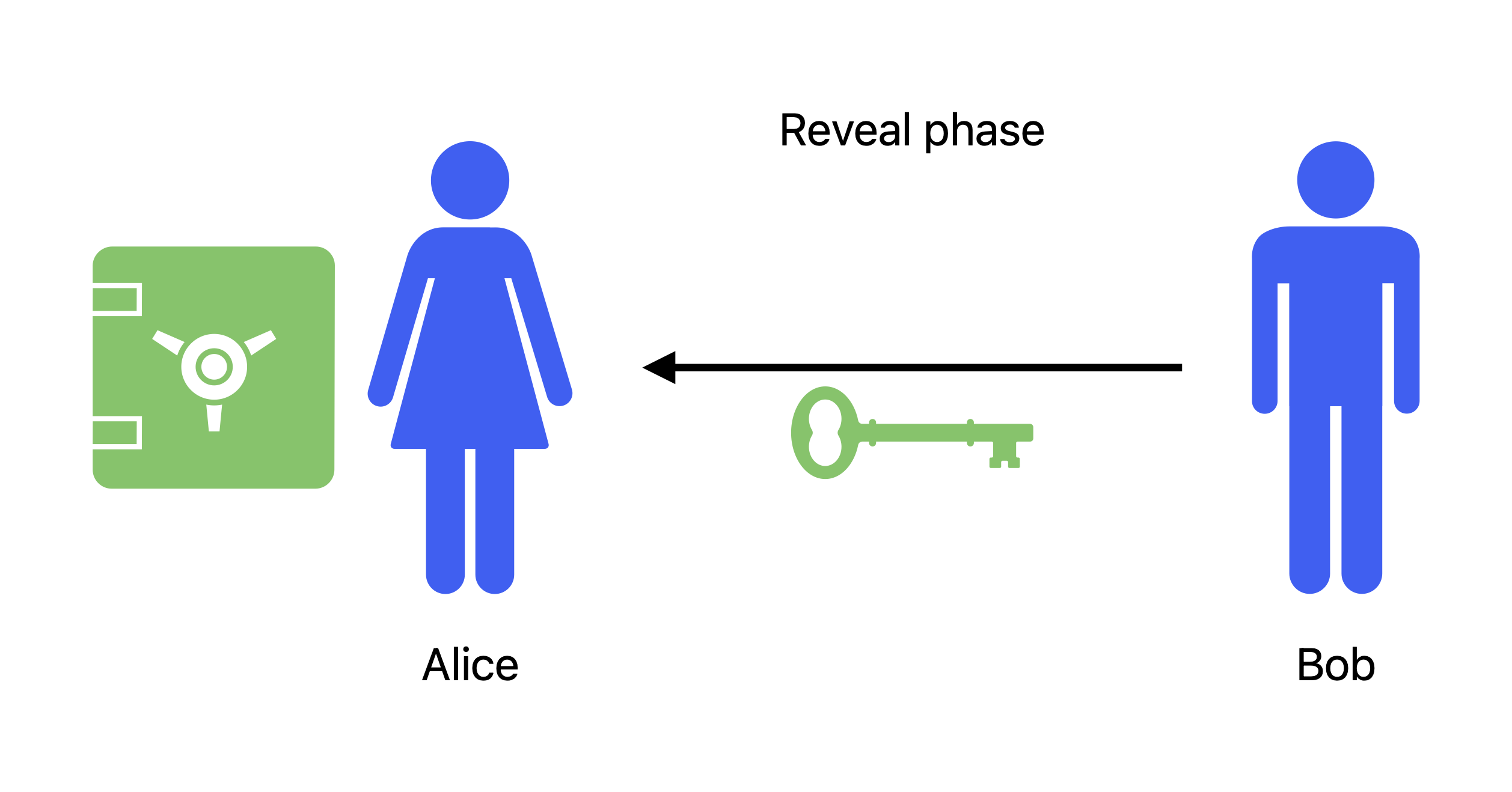
Figure 4
Alice and Bob just built a new instance of a commitment scheme (CS), in which Bob was able to securely commit to his secret order and later reveal it without being able to change his mind once Alice announced her guess.
Hash-based commitment scheme
A way to build a CS for digital applications consists in using a hash function H. The sender first computes the commitment C = H(s||o), where o is a random value called opening and s||o stands for the concatenation of the secret value and the opening. Then, the sender transmits C to the receiver. Later on, the sender reveals s and o and the receiver can indeed check that H(s||o) = C.
Protocol
| Homemade CS | Hash-based CS | |
|---|---|---|
| Commit phase | Bob places his secret order in a locked safe and gives the key to Alice. | The sender computes C = H (s||o) and transmits C to the receiver. |
| Reveal phase | Bob gives Alice the key and she can now observe the committed order. | The sender reveals s and o to the receiver and the latter can now check that H(s||o) matches C. |
Security properties
| Homemade CS | Hash-based CS | |
|---|---|---|
| Hiding | Alice is not able to peek inside the locked safe to get a hint about the secret order. | Due to the preimage resistance of H, the receiver cannot find s given C. |
| Binding | Once the safe is locked until it is opened, the order cannot be modified. | Due to the collision resistance of H, the sender cannot find two distinct pairs s||o and s’||o’ so that H(s||o) matches H(s’||o’). |
The role of commitments in Elusiv
When a user comes and deposits x funds of token y in the Elusiv shared pool, an associated commitment C is stored on-chain and derived as follows: C = H(x||y||n), where x||y||n stands for the concatenation of the fund amount x, the asset type y, and the nullifier n, which is a secret value kept hidden by the user depositing the funds. Later on, when the user wants to claim and spend the deposited funds, she proves that she knows the nullifier n to open the corresponding commitment C by deriving a zero-knowledge proof. It is crucial to keep nullifiers private to the user as those could be used to spend associated commitments. To make sure every commitment is claimed only once, the nullifiers must be stored on-chain too and checked if they have not been already used.
The hiding security property ensures that C does not leak information about the corresponding nullifier n, i.e. only the user possessing n can open the associated commitment. The binding property ensures that there is one single n that can be used to spend commitment C in addition to making sure a and y cannot be changed after depositing.
Zero-Knowledge Proofs
Homemade zero-knowledge proofs
Alice and Bob on their Friday night decide to play a few games of Where is Waldo?
During that game, Bob finds Waldo first but he does not want to reveal where he is. He wants to make sure Alice trusts him and does not think he tries to cheat once more, so Bob decides to derive a zero-knowledge proof (ZKP) for Alice, where he acts as the prover and Alice the verifier.
Bob covers the Where is Waldo?-map with huge cardboard that contains a tiny hole, enough to see Waldo through it and nothing more (Figure 5). As Bob found Waldo first, he can place the cardboard and show Waldo through the hole to Alice. First, it is clear that Bob knows the location of Waldo on the map, second, he just proved it without revealing the actual location to Alice as the Where is Waldo? could be located in any position under the cardboard.
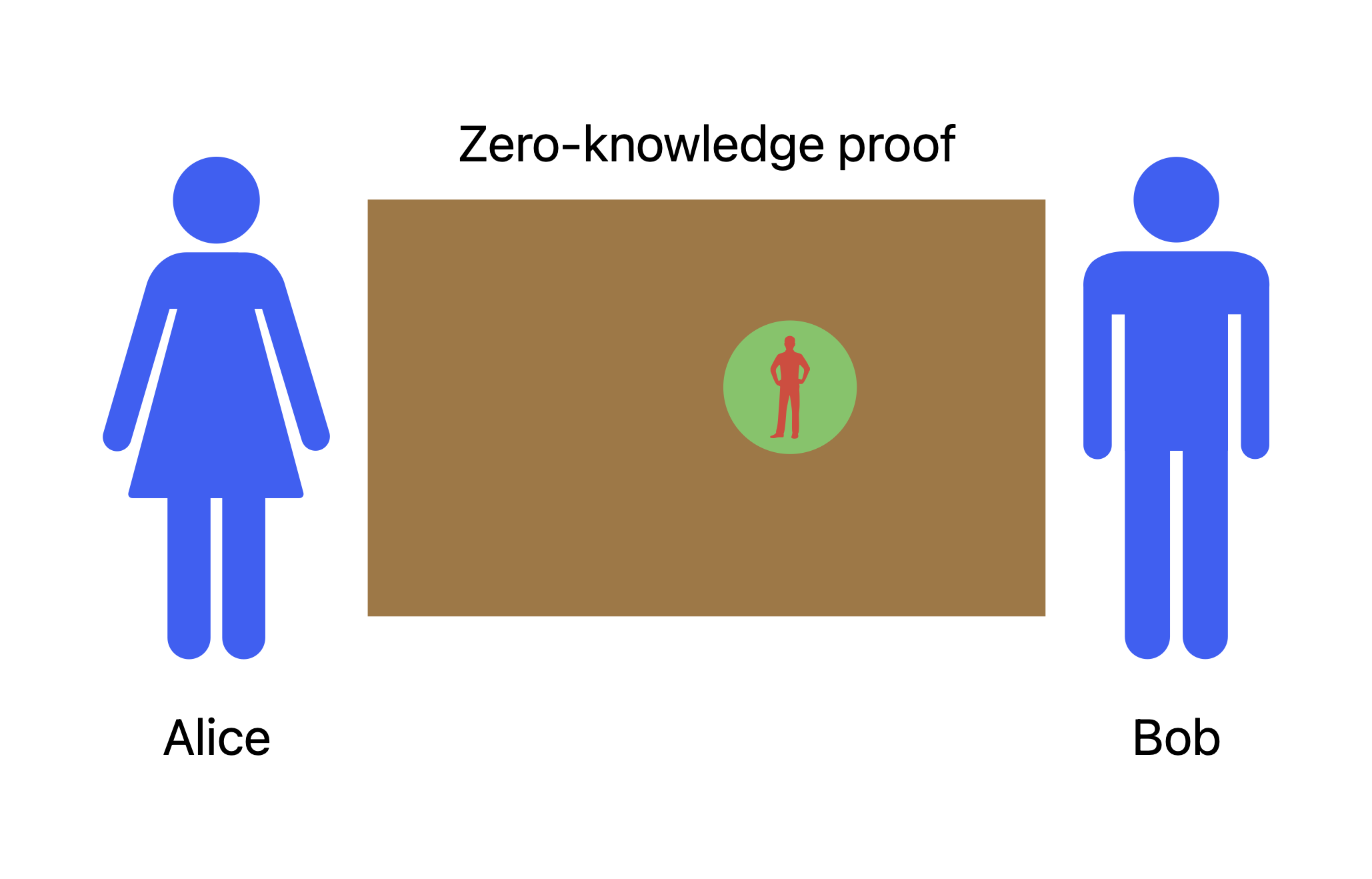
Figure 5
General zero-knowledge proofs
We use the following notation to concisely describe the private inputs x1, x2,.. and statements s1(x1, x2,...), s2(x1, x2,...),... that hold in a ZKP: ZKP{(x1, x2,...): s1 ^ s2 ^...}.
Security properties
| Homemade ZKP | General ZKP | |
|---|---|---|
| Completeness | Bob found Waldo, he is, therefore, able to show it through the hole to Alice. | If a prover possesses the knowledge, the verifier will be convinced of it. |
| Soundness | If Bob could not find Waldo, there is no way he could cheat and show it through the hole. | If a prover does not possess the knowledge, he cannot cheat and convince the verifier of the opposite. |
| Zero-knowledge | Bob reveals nothing more about Waldo than the fact he knows where it is. | If a prover convinces a verifier of his knowledge, then the proof does not reveal more than the fact he possesses that knowledge. |
The role of zero-knowledge proofs in Elusiv
ZKPs in Elusiv are of the form of zk-SNARKs, which stands for zero-knowledge Succinct Non-interactive ARguments of Knowledge with the Groth16 algorithm. ZK-SNARKs are a technique for deriving ZKPs to prove that a given computation was properly executed while keeping the inputs private. Succinct describes proofs’ short size and quick verification time. Non-interactive allows the prover to derive a proof without needing to interact with the verifier.
In the role of commitments in Elusiv, we mentioned that to claim unspent commitments, users need to prove they know their associated nullifiers. A trivial solution would be to reveal it, but this is not a very good way of doing it. First, it would break the privacy of users depositing and spending their funds. One could link deposits to commitments to the revealed nullifiers to track how a user is spending her funds. Second, the revealed nullifier could be intercepted by an adversary that could then spend the associated commitment before the user.
ZKPs come to the rescue! These allow the user to, instead of publicly revealing the nullifier n of a commitment C = H(x||y||n), generate a proof that embeds the knowledge of this secret value without leaking information about the latter: ZKP{(n), C = H(x||y||n)}. As soon as the user is no longer revealing the secret value, he does not fear an adversary linking it to the associated commitment or intercepting it.
The challenge that arises when users do not reveal nullifiers is not being able to store them on-chain, which poses the problem of checking that users are not double-spending their funds (by reusing nullifiers). In practice, we do not use the nullifier directly but we commit to a hash of n such as n0 = H(0||n) and later store n1 = H(1||n). The hiding property of hash functions ensures that stored hashed nullifiers cannot be linked to the corresponding commitments, therefore, breaking the link from deposits to spendings. Only the user can generate n0 and n1, therefore, instead of trusting her, she is asked to provide a ZKP that these values are properly formed. When depositing, we can check ZKP{(n): n0 = H(0||n)} and derive C = H(x||y||n0). When spending, we can check ZKP{(n): C = H(x||y||n0) ^ n1 = H(1||n)} before storing n1 on-chain.
Cryptographic Hash Functions
The Plant Magic Company
Alice and Bob are big fans of smoothies. Little do they know that puréeing ingredients in a blender is an amazing analogy to how cryptographic hash functions work. You can throw in a variety of ingredients like fruits, vegetables, and liquids, and the blender will chop them up and blend them until they become a smoothie. Similarly, cryptographic hash functions H take in any kind of digital data as bytes b and blend it into a deterministic, unique, scrambled chain of characters called a hash h = H(b). Popular hash function families include SHA for a wide variety of widespread cryptographic applications and Poseidon for zero-knowledge applications, as the latter efficiently allows for generating zero-knowledge proofs on the inputs being hashed.
Security properties
| Blender analogy | Hash function | |
|---|---|---|
| Preimage resistance | Given a smoothie, it is impossible to retrieve the exact original recipe. | Given h, it is impossible to retrieve the bytes b that were hash as h = H(b). |
| Second preimage resistance | Given a smoothie, it is impossible to find a recipe different from the original one that gives the same result. | Given h, it is impossible to find b’ such that h = H(b) = H(b’). |
| Collision-free | It is impossible to find two different recipes that blend into the same smoothie. | It is impossible to find a pair b and b’ such that H(b) = H(b’) |
The role of hash functions in Elusiv
Hash functions are the Swiss Army Knife of the cryptography world due to the essential role they play to derive cryptographic primitives and protocols. Hash functions play a natural role in Elusiv, for instance, in our commitment scheme and zero-knowledge proofs.